使用 Groovy™ 解决背包问题
发布时间:2024-02-09 03:00PM
背包问题是一个组合优化问题。给定一组物品,每个物品都有其重量和价值,确定将哪些物品放入背包(或其他容器)中,以在不超过给定重量限制的情况下最大化背包内的总价值。

案例研究
对于我们的案例研究,我们将从将宝石放入背包开始。宝石具有以下特征:
| 索引 | 重量 | 价值 |
|---|---|---|
0 |
1 |
1 |
1 |
2 |
5 |
2 |
3 |
10 |
3 |
5 |
15 |
4 |
6 |
17 |
宝石可以放入背包,也可以不放入。这被称为问题的 0/1 背包变体。我们稍后会介绍其他变体。
我们的目标是找出将哪些宝石放入背包以使价值最大化。

暴力破解
我们可能采取的第一种方法是简单地尝试所有可能的组合,丢弃任何超过重量限制的组合,然后找出剩余组合中的最大值。
一种方法是生成所有可能的索引组合。然后,选择满足背包重量限制的组合。然后,找到产生最高价值的组合,如下所示:
int[] values = [1, 5, 10, 15, 17] // Gem values
int[] weights = [1, 2, 3, 5, 6] // Weights
int W = 10
var totalValue = { it*.v.sum() }
var withinLimit = { it*.w.sum() <= W }
var asTriple = { [i:it, w:weights[it], v:values[it]] }
var best = weights
.indices
.collect(asTriple)
.subsequences()
.findAll(withinLimit)
.max(totalValue)
println "Total value for capacity $W = ${totalValue(best)}"
println "Gems taken: ${best*.i}"
println "Gem weights: ${best*.w}"更详细地说,我们首先定义三个辅助闭包:totalValue、withinLimit 和 asTriple。将数据收集到地图列表(三元组)中不是必需的,但可以简化后续处理。获得数据后,我们找到子序列,保留在重量限制内的子序列,然后找到最大值。
运行此脚本会产生以下输出:
Total value for capacity 10 = 30 Gems taken: [1, 2, 3] Gem weights: [2, 3, 5]
虽然这足够简单,但它没有提供很多优化机会。对于像我们案例研究这样的小问题,优化并不重要,但对于更大的问题,组合数量可能会呈指数级增长,我们需要记住这一点。
相反,让我们考虑一种递归解决方案,它允许我们对于超过背包最大重量限制的情况更早地退出:
int solve(int[] w, int[] v, int W) {
knapsack(w, v, v.length, W)
}
int knapsack(int[] w, int[] v, int n, int W) {
if (n <= 0) {
0
} else if (w[n - 1] > W) {
knapsack(w, v, n - 1, W)
} else {
[knapsack(w, v, n - 1, W),
v[n - 1] + knapsack(w, v, n - 1, W - w[n - 1])].max()
}
}
int[] values = [1, 5, 10, 15, 17] // Gem values
int[] weights = [1, 2, 3, 5, 6] // Weights
[6, 8, 10].each {
println "Total value for capacity $it = ${solve(weights, values, it)}"
}在这里,我们考虑每颗宝石(对于给定阶段,宝石 n,或索引 n - 1)。有两种路径可以计算,一种是宝石包含在内,另一种是宝石排除在外。我们记住从这两条路径返回的最大值并继续处理。当宝石包含在内时,我们解决一个较小的问题:将剩余的宝石放入一个概念上较小的背包中。如果将宝石放入背包导致重量超过限制,那么我们可以从进一步的处理中丢弃该路径。
将上述过程可视化为一棵解决方案树(容量为 10 时显示)会很有用:
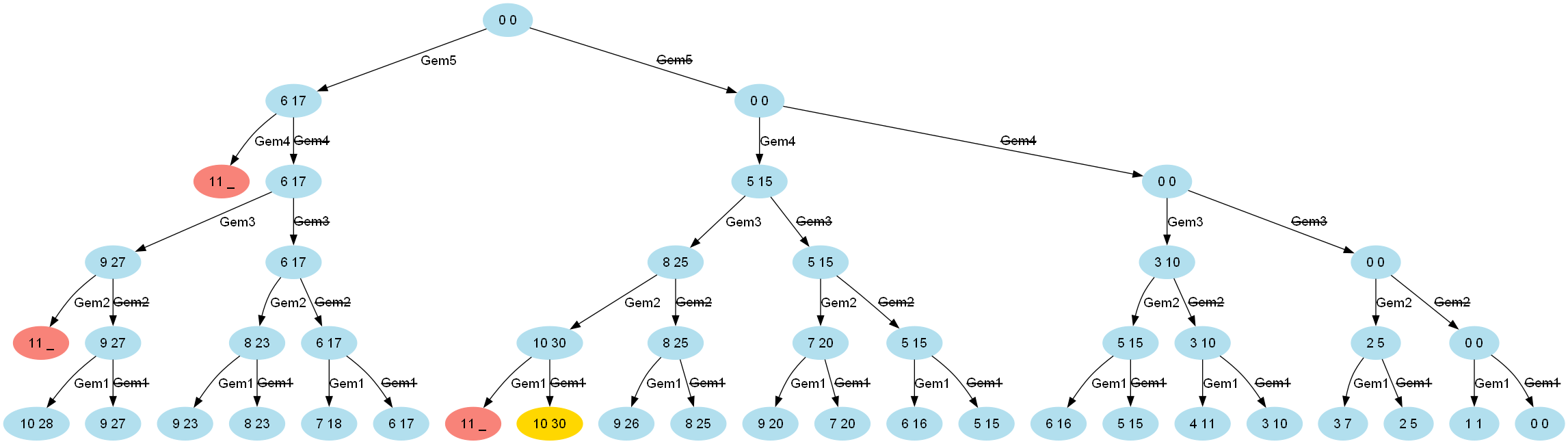
浅红色节点表示可以跳过解决方案树的后续处理的地方。
我们在这里计算了 3 种不同背包重量限制(6、8 和 10)的结果。输出如下:
Total value for capacity 6 = 17 Total value for capacity 8 = 25 Total value for capacity 10 = 30
我们不会处理 32 种组合(我们的 5 颗宝石是 2^5),而只会处理 11、16 和 21 种组合,其中当最大重量限制分别为 6、8 和 10 时,两条路径都被遍历。
更重要的是,我们将有进一步的优化可能性。一个快速的胜利是记忆化(缓存)调用 knapsack 方法的结果。Groovy 使这变得容易。与上面唯一的区别是添加了 @Memoized 注解:
@Memoized
int knapsack(int[] w, int[] v, int n, int W) {
if (n <= 0) {
0
} else if (w[n - 1] > W) {
knapsack(w, v, n - 1, W)
} else {
[knapsack(w, v, n - 1, W),
v[n - 1] + knapsack(w, v, n - 1, W - w[n - 1])].max()
}
}运行此操作会产生与以前相同的结果,但 knapsack 方法的执行次数从 44 次减少到 32 次(仅在计算重量限制为 10 的背包时),并从 107 次减少到 49 次(在计算 6、8 和 10 时)。
使用分支定界法
另一种常用的优化技术是分支定界法。它是分治法的一種特殊形式;通过将大问题分解为小问题来解决它。
分治法与我们上面用于递归解决方案的方法类似,但分支定界法我们执行更智能的消除。在处理分支的子节点之前,会根据一些最优解的上限和下限估计值检查分支。如果我们可以确定沿着该路径前进不可能比沿着其他替代路径前进更好,则会终止给定路径的处理。对于背包问题,我们可以通过找到最佳“贪婪”解决方案来计算这些边界,如果允许我们使用给定背包物品的零星数量的话。我们将把零星数量作为此博客中的最后一个示例。事实证明我们可以非常高效地计算它们。
首先,我们将创建一个 Item 记录来保存我们的重量和价值。
record Item(int weight, int value) {}接下来,我们将创建一个 Node 来保存解决方案树中特定点上候选解决方案的当前状态信息。
@Canonical
class Node {
int level, value, weight
public int bound
static Node next(Node parent) {
new Node(parent.level + 1, parent.value, parent.weight)
}
}接下来,bound 方法使用最优(贪婪)算法计算重量。这需要我们允许宝石的零碎部分才能精确,但在我们的例子中,我们只是将其用作一个边界。可以将其视为在考虑最佳和最坏情况下的估计。
int bound(Node u, int n, int W, List<Item> items) {
if (u.weight >= W)
return 0
int valueBound = u.value
int j = u.level + 1
int totalWeight = u.weight
while (j < n && totalWeight + items[j].weight <= W) {
totalWeight += items[j].weight
valueBound += items[j].value
j++
}
if (j < n)
valueBound += (int) ((W - totalWeight) * items[j].value / items[j].weight)
valueBound
}现在,我们的背包方法将根据每单位重量的最高价值对宝石进行排序,然后进行处理,同时在每一步跟踪边界。
int knapsack(int W, List<Item> items, int n) {
items.sort { it.value / it.weight }
var q = new PriorityQueue<>((a, b) -> b.bound <=> a.bound)
Node u, v
q.offer(new Node(-1, 0, 0))
int bestValue = 0
while (q) {
u = q.poll()
if (u.level == n - 1)
continue
else
v = Node.next(u)
v.weight += items[v.level].weight
v.value += items[v.level].value
if (v.weight <= W && v.value > bestValue)
bestValue = v.value
v.bound = bound(v, n, W, items)
if (v.bound > bestValue)
q.offer(v)
v = Node.next(u)
v.bound = bound(v, n, W, items)
if (v.bound > bestValue)
q.offer(v)
}
bestValue
}
int W = 10
int[] values = [1, 5, 10, 15, 17] // Gem values
int[] weights = [1, 2, 3, 5, 6] // Weights
var items = values.indices.collect {
new Item(weights[it], values[it])
}
println "Total value for capacity $W = ${knapsack(W, items, values.length)}"它的可视化效果是这样(容量为 10):
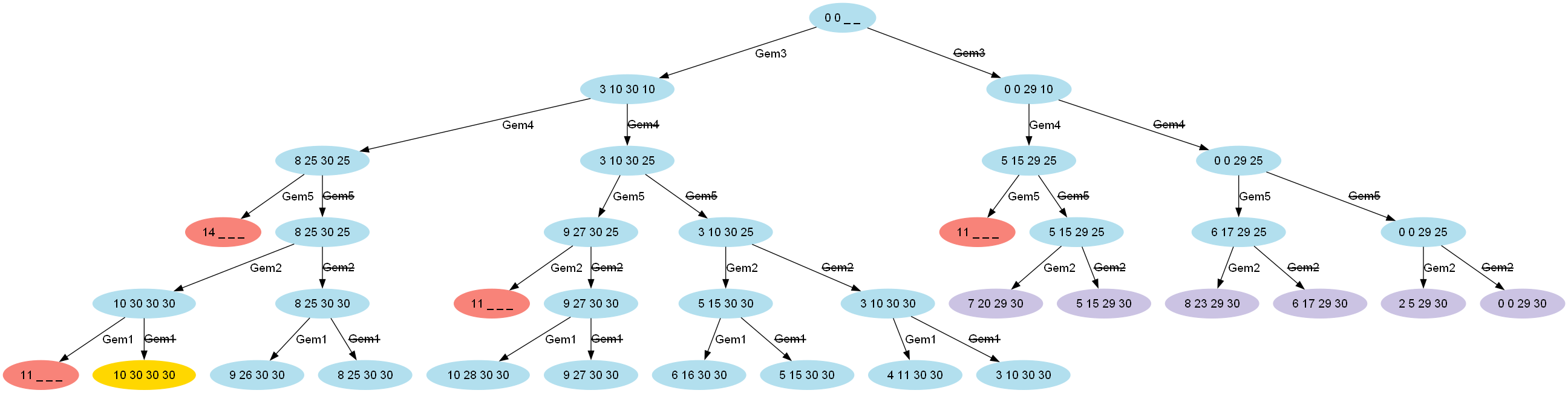
我们应该注意到,除了丢弃超过重量限制的不可行路径(浅红色)之外,我们现在还丢弃了无果的路径(浅紫色),我们的边界值告诉我们这些路径永远不可能超过我们已经知道的某个替代的最佳路径。
它有以下输出:
Total value for capacity 10 = 30
使用动态规划
您可以将动态规划视为分支定界法的一种特殊情况。它也可以被认为是与我们之前看到的记忆化类似。在这种情况下,我们不是让 Groovy 为我们提供缓存,而是自己在 dp 数组中跟踪它:
int solve(int[] v, int[] w, int W) {
knapsack(new Integer[v.length][W+1], v, w, W, 0)
}
int knapsack(Integer[][] dp, int[] v, int[] w, int W, int n) {
if (W <= 0 || n >= v.length) {
return 0
}
if (dp[n][W]) {
return dp[n][W]
}
int tryN = w[n] > W ? 0 : v[n] + knapsack(dp, v, w, W - w[n], n + 1)
int skipN = knapsack(dp, v, w, W, n + 1)
dp[n][W] = max(tryN, skipN)
}
int[] values = [1, 5, 10, 15, 17] // Gem values
int[] weights = [1, 2, 3, 5, 6] // Weights
[6, 8, 10].each {
println "Total value for capacity $it = ${solve(values, weights, it)}"
}为了解决背包问题,我们将其分解为更小的部分。如果已经缓存了较小部分的解决方案,我们就使用缓存值。由于我们构建问题的方式,我们实际上共享了不同背包大小的缓存结果。
当我们运行此脚本时,它会生成以下输出:
Total value for capacity 6 = 17 Total value for capacity 8 = 25 Total value for capacity 10 = 30
像大多数事情一样,在使用动态规划时我们也有多种选择。这是一个替代变体,它保留了第二个数组来跟踪所取的宝石:
int[] values = [1, 5, 10, 15, 17] // Gem values
int[] weights = [1, 2, 3, 5, 6] // Weights
int W = 10
int N = values.length
int[][] dp = new int[N + 1][W + 1]
boolean[][] sol = new boolean[N + 1][W + 1]
for (int n = 1; n <= N; n++) {
for (int w = 1; w <= W; w++) {
int skipN = dp[n - 1][w]
int tryN = weights[n - 1] > w ? 0 : values[n - 1] + dp[n - 1][w - weights[n - 1]]
dp[n][w] = max(skipN, tryN)
sol[n][w] = tryN > skipN
}
}
println "Total value for capacity $W = ${dp[N][W]}"
def taken = []
for (int i = N, j = W; j > 0; i--) {
if (sol[i][j]) {
taken << i - 1
j -= weights[i - 1]
}
}
println "Gems taken: $taken"如果只想要最终价值,我们之前的变体将稍微快一点,并且占用更少的内存。如果跟踪所取的宝石很重要,那么这种变体将是一种可行的方法。
它产生以下输出:
Total value for capacity 10 = 30 Gems taken: [3, 2, 1]
使用 BitSets
在使用动态规划时,我们的二维 dp 数组对于大型问题可能会占用大量内存。在这种情况下,我们可以使用位集而不是数组,像这样:
int[] values = [1, 5, 10, 15, 17] // Gem values
int[] weights = [1, 2, 3, 5, 6] // Weights
int W = 10
var N = weights.size()
var nums = 0L..<(1L << N)
var totalValue = nums
.collect{ BitSet.valueOf(it) }
.findAll{ mask -> mask.stream().map(idx -> weights[idx]).reduce(0, Integer::sum) <= W }
.collect{ mask -> nums.indices.sum{ idx -> mask[idx] ? values[idx] : 0 } }
.max()
println "Total value for capacity $W = $totalValue"在这里,我们使用位集来跟踪候选解决方案中的宝石组合。这可能看起来有点不寻常,但在我们的案例中却能发挥作用。
它有以下输出:
Total value for capacity 10 = 30
通常,位集不仅用于节省内存,还因为对于某些问题,我们可以对整个位集执行操作。您可以将其视为批量操作,与对布尔数组等执行此类操作相比,它具有免费并行性。
我们可以通过添加一个初步的优化步骤来展示这种操作的一个简单示例。我们将使用一个简单的技巧,它可以使用位移位找到一组数字的所有可能和。如果最大重量(此示例中为 10)不在可能和的列表中——我们使用 maskW 常量发现这一点,那么我们就丢弃该组合。为了简单起见,我们在这里使示例保持简单,但请注意,这种粗略的优化有排除有效候选的可能性。例如,理论上最大值可能是重量为 8 或 9。
int[] values = [1, 5, 10, 15, 17] // Gem values
int[] weights = [1, 2, 3, 5, 6] // Weights
int W = 10
var N = weights.size()
var maskW = 1L << W
var nums = 0L..<(1L << N)
var totalValue = nums
.collect{ BitSet.valueOf(it) }
.findAll{ mask -> mask.stream().reduce(1) {a, b -> a | a << weights[b] } & maskW }
.findAll{ mask -> mask.stream().map(idx -> weights[idx]).reduce(0, Integer::sum) <= W }
.collect{ mask -> nums.indices.sum{ idx -> mask[idx] ? values[idx] : 0 } }
.max()
println "Total value for capacity $W = $totalValue"对于本案例研究,它具有相同的输出,所以幸运的是,我们粗略的优化步骤并没有拒绝最佳解决方案。
在此示例中,我们只是移动了一个整数。根据具体问题,我们可能希望移动一个长整型或位集。Groovy 5 添加了对位集的 <<(左移)、>>(右移)和 >>>(无符号右移)运算符的支持。这种功能将使使用 Groovy 处理此类问题变得更加方便。
使用约束编程
我们认为我们还会为示例增添趣味,并说明所谓的有界背包问题。现在,我们不只是选择或不选择宝石,而是将宝石视为现成的商品,重量和价值将适用于特定类型的所有宝石。
通常,我们可以根据需要获取任意数量的特定类型的宝石(这将是无界的),或者像我们这里一样,获取任意数量的特定类型的宝石,但有一定上限。
在我们的示例中,我们将求解器领域变量的边界设置为介于 0 和 W 之间。我们可以轻松地将上限设置为 1,然后我们就回到了 0/1 背包问题。
int[] values = [1, 5, 10, 15, 17] // Gem values
int[] weights = [1, 2, 3, 5, 6] // Weights
int W = 10
int unbounded = 100000
var counts = new IntVar[values.length]
var found = false
new Model('KnapsackProblem').with {
counts.indices.each(i -> counts[i] = intVar("count$i", 0, W))
scalar(counts, weights, '<=', W).post()
var total = intVar("Total value for capacity $W (unbounded)", 0, unbounded)
scalar(counts, values, '=', total).post()
setObjective(MAXIMIZE, total)
while (solver.solve()) {
found = true
println "$total, $counts"
}
}
if (!found) println 'No solution'我们维护一个求解器变量 counts 数组,对变量应用大量约束,然后告诉求解器最大化 total 变量。
当我们运行此脚本时,它会生成以下输出:
Total value for capacity 10 (unbounded) = 25, [count0 = 0, count1 = 5, count2 = 0, count3 = 0, count4 = 0] Total value for capacity 10 (unbounded) = 30, [count0 = 0, count1 = 2, count2 = 2, count3 = 0, count4 = 0] Total value for capacity 10 (unbounded) = 31, [count0 = 1, count1 = 0, count2 = 3, count3 = 0, count4 = 0]
在这里,求解器正在寻找满足我们指定问题条件的解决方案,然后尝试找到更好的解决方案。我们应该注意到,由于我们允许每种宝石不止一个,因此我们的答案 (31) 高于我们之前的最佳答案 (30) 并不奇怪。
如果我们不想接收所有解决方案,我们可以简单地要求最佳解决方案,或者为求解器提供更好的问题搜索提示,以便更早地获得最佳答案。
事实证明,我们在这里为解决背包问题而设置的约束集非常常见,因此 Choco 有一个内置的 knapsack 方法,可以为我们设置多个约束。我们可以像这样使用它:
int[] values = [1, 5, 10, 15, 17] // Gem values
int[] weights = [1, 2, 3, 5, 6] // Weights
int W = 10
int unbounded = 100000
var counts = new IntVar[values.length]
var found = false
new Model('KnapsackProblem').with {
counts.indices.each(i -> counts[i] = intVar("count$i", 0, W))
var totalValue = intVar("Total value for capacity $W (unbounded)", 0, unbounded)
var totalWeight = intVar("Total weight taken", 0, W)
knapsack(counts, totalWeight, totalValue, weights, values).post()
setObjective(MAXIMIZE, totalValue)
while (solver.solve()) {
found = true
println "$totalValue, $totalWeight, $counts"
}
}
if (!found) println 'No solution'运行时输出如下:
Total value for capacity 10 (unbounded) = 30, Total weight taken = 10, [count0 = 0, count1 = 2, count2 = 2, count3 = 0, count4 = 0] Total value for capacity 10 (unbounded) = 31, Total weight taken = 10, [count0 = 1, count1 = 0, count2 = 3, count3 = 0, count4 = 0]
使用 OrTools
其他库也有内置的背包求解器。这是使用 OrTools 库的另一个实现:
Loader.loadNativeLibraries()
var solver = new KnapsackSolver(KNAPSACK_MULTIDIMENSION_BRANCH_AND_BOUND_SOLVER, "knapsack")
long[] values = [1, 5, 10, 15, 17]
long[][] weights = [[1, 2, 3, 5, 6]]
long[] capacities = [10]
solver.init(values, weights, capacities)
long computedValue = solver.solve()
println "Total value for capacity ${capacities[0]} = " + computedValue
var packedItems = []
var packedWeights = []
int totalWeight = 0
values.indices.each { i ->
if (solver.bestSolutionContains(i)) {
packedItems << i
packedWeights << weights[0][i]
totalWeight += weights[0][i]
}
}
println "Actual weight: $totalWeight"
println "Gems taken: $packedItems"
println "Gem weights: $packedWeights"运行时输出如下:
Total value for capacity 10 = 30 Actual weight: 10 Gems taken: [1, 2, 3] Gem weights: [2, 3, 5]
使用 Jenetics
我们还可以使用遗传算法来寻找解决方案。在基于遗传算法创建解决方案时,会发生一系列步骤,这些步骤模拟自然进化。我们通常从一些随机猜测开始,我们将其视为第一代后代。我们有函数来测试个体的适应度,根据当前一代选择新一代后代的流程,突变步骤等等。
我们将首先创建一个记录来跟踪我们的重量和价值。
record Item(int weight, int value) implements Serializable {}我们将创建一个 Knapsack 类来跟踪状态并提供我们的适应度函数。
class Knapsack implements Problem<ISeq<Item>, BitGene, Integer> {
private final Codec<ISeq<Item>, BitGene> codec
private final double knapsackSize
Knapsack(ISeq<Item> items, int knapsackSize) {
codec = Codecs.ofSubSet(items)
this.knapsackSize = knapsackSize
}
@Override
Function<ISeq<Item>, Integer> fitness() {
(items) -> {
var sum = items.inject(new Item(0, 0)) { acc, next ->
new Item(acc.weight + next.weight, acc.value + next.value)
}
sum.weight <= knapsackSize ? sum.value : 0
}
}
@Override
Codec<ISeq<Item>, BitGene> codec() { codec }
}我们创建了遗传算法引擎并对其进行配置,以确定如何选择下一代,以及可能使用哪些突变(如果有)来提供随机改变。
我们还将创建一个 log 函数,以便在我们生成各种世代时输出一些信息。
这是脚本:
int W = 10
int[] values = [1, 5, 10, 15, 17] // Gem values
int[] weights = [1, 2, 3, 5, 6] // Weights
var items = [weights, values].transpose().collect { w, v -> new Item(w, v) }
var iSeq = items.stream().collect(ISeq.toISeq())
var knapsack = new Knapsack(iSeq, W)
var engine = Engine.builder(knapsack)
.populationSize(8)
.survivorsSelector(new TournamentSelector<>(3))
.offspringSelector(new RouletteWheelSelector<>())
.alterers(
new Mutator<>(0.1),
new SinglePointCrossover<>(0.2),
new MultiPointCrossover<>(0.1))
.build()
var log = { EvolutionResult er ->
var avg = er.population().average{ it.fitness() }
var best = er.bestFitness()
printf "avg = %5.2f, best = %d%n", avg, best
}
var best = engine.stream()
.limit(bySteadyFitness(8))
.limit(30)
.peek(log)
.collect(toBestPhenotype())
println best运行时会产生以下输出:
avg = 18.88, best = 23 avg = 21.00, best = 25 avg = 22.00, best = 25 avg = 22.63, best = 25 avg = 25.63, best = 30 avg = 27.50, best = 30 avg = 27.63, best = 30 avg = 24.38, best = 30 avg = 22.50, best = 30 avg = 26.25, best = 30 avg = 30.00, best = 30 avg = 30.00, best = 30 [00001110] -> 30
由于它是随机的,后续运行可能会产生不同的结果。
avg = 16.75, best = 27 avg = 17.13, best = 23 avg = 18.00, best = 23 avg = 21.38, best = 27 avg = 24.00, best = 27 avg = 24.88, best = 27 avg = 22.50, best = 27 avg = 26.88, best = 27 [00010100] -> 27
正如我们在这里看到的,并非所有遗传算法问题都能保证获得最优解。
我们应该注意到,虽然这个过程涉及各种随机方面,并且我们有时可能会淘汰最佳个体,但如果我们的算法配置正确,我们应该会看到平均和最佳适应度值随着时间的推移而上升。
使用贪婪选择
我们将要看的最后一个例子是“最优”或“贪婪”解决方案。在这里,我们按照价值/重量比的最佳顺序选择物品。如果允许分数价值大于 1,我们只需使用此排序列表中的第一个物品,但在这里,任何物品的最大值为 1。
对于这个问题,你可能不会把它看作是宝石(宝石可能很难分割,或者至少分割后不会大幅贬值),而会把它看作是异国香料,或其他可以轻易分割的贵重物品。
这是代码:
int[] values = [1, 5, 10, 15, 17] // Gem values
int[] weights = [1, 2, 3, 5, 6] // Weights
var ratios = values.indices.collect { values[it] / weights[it] }.withIndex().sort { -it[0] }
int W = 10
Map<Integer, BigDecimal> taken = [:]
var remaining = W
while (remaining && ratios) {
var next = ratios.head()
var index = next[1]
if (remaining >= weights[index]) {
taken[index] = 1
remaining -= weights[index]
} else {
taken[index] = remaining / weights[index]
break
}
ratios = ratios.tail()
}
var total = taken.collect{ index, qty -> values[index] * qty }.sum()
println taken
printf 'Total value for capacity %d (with fractions) = %6.3f%n', W, total运行时输出如下:
[2:1, 3:1, 4:0.3333333333] Total value for capacity 10 (with fractions) = 30.667
当我们允许可分割的贵重物品时,能够获得高于 30 的价值并不出乎意料。
更多信息
结论
我们已经看到了如何使用几种方法在 Groovy 中解决背包问题。在参考文献中,甚至有更多奇特的算法可以用来解决背包问题。如果您有使用 Groovy 解决背包问题的好方法,请告诉我们,我们可以将其添加到此博客中!
