使用 Groovy™ 和 Choco、JaCoP、OR-Tools 解决密码算术谜题
发布时间:2022-09-05 01:43PM
简介
在编写问题解决方案时,我们经常努力隐藏实现细节。在面向对象 (OO) 编程中,我们可能会构建一个具有精心设计的丰富方法的分层类,以便我们的最终解决方案可以用我们领域模型中简单的名词和动词(方法和类实例)来表达。在应用函数式编程范式时,我们将努力强调输入和输出之间的关系,并隐藏副作用和迭代步骤。
约束编程(与逻辑编程属于同一家族)也致力于隐藏细节。它不是表达迭代实现,而是专注于表达解决方案的声明性属性。求解器负责制定精确的实现步骤。
使用约束编程时,我们开发一个模型,该模型由变量、每个变量可能持有的值域以及变量之间的附加约束组成。求解器完成所有工作。它可能采用启发式搜索、推理、传播、对称和回溯来查找可能的解决方案。我们可能能够(或希望、或需要)指导求解器使用哪些技术和策略。约束编程已用于解决各种问题,包括调度问题,并且擅长处理组合可能性过多而其他数学优化方法无法解决的问题。经常使用的示例问题包括数独和 Wordle 求解器、N 皇后问题以及其他类型的谜题。我们只看密码算术谜题。
密码算术问题
密码算术问题(也称为字母算术、文字算术、密码和词语加法)是一种数学游戏,其中数学方程中的数字被字母替换。传统上,每个字母通常代表一个唯一的数字,并且数字不能以零开头。如果我们看一个示例问题
T |
O |
||
+ |
G |
O |
|
= |
O |
U |
T |
我们可以手动推断出解决方案
-
T、O、U 和 G 必须都不同(游戏规则)
-
T、G 和 O 将介于 1 到 9 之间,U 介于 0 到 9 之间(游戏规则)
-
如果我们将两个最大的两位数相加(99 + 99),我们会得到 198,所以O 必须是 1
-
看最右边的“个位”列,1 + 1 等于 2,所以T 必须是 2
-
看“十位”列,我们知道有进位 1(因为 O 是 1),并且我们知道 T 是 2,所以 G 必须是 8 或 9。如果 G 是 9,U 将是 1,但它不能与 O 相同,所以G 必须是 8,U 必须是 0。
手动求解时,我们通常会推理单个列并考虑“进位”到下一列。我们稍后会回到这一点,但首先,让我们看一个稍微大一点的问题
S |
E |
N |
D |
||
+ |
M |
O |
R |
E |
|
= |
M |
O |
N |
E |
Y |
暴力破解
这个问题不大,所以我们可以用暴力破解。我们简单地尝试谜题中字母的所有可能值
for (s in 1..9)
for (e in 0..9)
for (n in 0..9)
for (d in 0..9)
for (m in 1..9)
for (o in 0..9)
for (r in 0..9)
for (y in 0..9)
if ([s, e, n, d, m, o, r, y].toSet().size() == 8) {
def send = 1000 * s + 100 * e + 10 * n + d
def more = 1000 * m + 100 * o + 10 * r + e
def money = 10000 * m + 1000 * o + 100 * n + 10 * e + y
if (send + more == money) {
println "s = $s, e = $e, n = $n, d = $d"
println "m = $m, o = $o, r = $r, y = $y"
}
}但这效率不高。它计算了 8100 万个变量组合,然后只跳过了其中的 150 万个(因为大多数不是唯一的)。总共可能在几十秒内执行完毕。
或者,Groovy 支持计算排列,因此我们可以将解决方案简化为一个简单的 for 循环(带有一些测试以消除无用的迭代)
def digits = 0..9
for (p in digits.permutations()) {
if (p[-1] < p[-2]) continue
def (s, e, n, d, m, o, r, y) = p
if (s == 0 || m == 0) continue
def send = 1000 * s + 100 * e + 10 * n + d
def more = 1000 * m + 100 * o + 10 * r + e
def money = 10000 * m + 1000 * o + 100 * n + 10 * e + y
if (send + more == money) {
println "s = $s, e = $e, n = $n, d = $d"
println "m = $m, o = $o, r = $r, y = $y"
}
}这有一个优点,只生成唯一的组合。它将在几秒钟内执行完毕。
运行这些解决方案中的任何一个都会得到
s = 9, e = 5, n = 6, d = 7 m = 1, o = 0, r = 8, y = 2
使用约束编程
对于暴力破解方法,我们有一个条件,用于检查任何潜在的候选答案是否是正确的解决方案。我们必须非常明确地说明我们希望如何创建潜在的候选。对于约束编程,我们改为定义变量来表示问题,这些变量上的任何已知边界,并且我们指定解决方案的任何其他已知属性,在我们的例子中,这将类似于我们之前需要检查答案是否正确的条件。让我们研究如何使用三个库来做到这一点,其中一个库有一个变体。
Choco
以下是使用 Choco 库的代码
new Model("SEND+MORE=MONEY").with {
def (S, M) = ['S', 'M'].collect { intVar(it, 1, 9) }
def (E, N, D, O, R, Y) = ['E', 'N', 'D', 'O', 'R', 'Y'].collect { intVar(it, 0, 9) }
allDifferent(S, E, N, D, M, O, R, Y).post()
IntVar[] ALL = [
S, E, N, D,
M, O, R, E,
M, O, N, E, Y ]
int[] COEFFS = [
1000, 100, 10, 1,
1000, 100, 10, 1,
-10000, -1000, -100, -10, -1 ]
scalar(ALL, COEFFS, "=", 0).post()
println solver.findSolution()
}我们定义了变量及其边界(域)。我们使用 allDifferent 全局约束来指定唯一性要求,并使用 scalar 约束来确保我们的变量乘以它们各自的标量系数等于 0。这使我们能够考虑特定变量是否代表“个位”列、“十位”列、“百位”列等。这捕获了“谜题加法”约束。然后我们要求求解器找到解决方案。我们也可以很容易地要求所有解决方案(如果存在多个)。
这是我们解决此类问题的典型方式。我们要么直接在变量之间定义约束,要么使用库可能支持的任何全局约束。如果我们的库不支持我们需要的约束,我们会找到一种方法使用多个更简单的约束来表达它。
最终结果是我们的代码比暴力破解方法更具声明性,并且在几十毫秒内找到解决方案。求解器具有解决此类谜题的非常有效的策略。
JaCoP
我们可以使用 JaCoP 解决同样的问题
def store = new Store()
def (S, M) = ['S', 'M'].collect { new IntVar(store, it, 1, 9) }
def (E, N, D, O, R, Y) = ['E', 'N', 'D', 'O', 'R', 'Y'].collect { new IntVar(store, it, 0, 9) }
var ctr = new Alldifferent(S, E, N, D, M, O, R, Y)
store.impose(ctr)
IntVar[] ALL = [
S, E, N, D,
M, O, R, E,
M, O, N, E, Y ]
int[] COEFFS = [
1000, 100, 10, 1,
1000, 100, 10, 1,
-10000, -1000, -100, -10, -1 ]
var lin = new LinearInt(ALL, COEFFS, "==", 0)
store.impose(lin)
var label = new DepthFirstSearch()
var select = new InputOrderSelect(store, ALL, new IndomainMin())
label.labeling(store, select)此 API 中存在一些细微差别,但几乎所有内容都与我们之前看到的有一对一的对应关系。我们在这里明确选择搜索策略和选择策略,而在 Choco 中,为我们选择了默认值。在两种情况下,显式创建此类类允许在需要时针对特定场景更改策略。
运行时,输出如下所示
Labeling has finished with return value of true DFS1: DFS([S = 9, E = 5, N = 6, D = 7, M = 1, O = 0, R = 8, Y = 2], InputOrder, (org.jacop.search.IndomainMin@45394b31))
我们可以看到这里的代码与执行时间非常相似。
OR-Tools
我们可以使用 OR-Tools 重复解决方案。这是代码
Loader.loadNativeLibraries()
new Solver('Send+More=Money').with {
def s = makeIntVar(1, 9, 's')
def e = makeIntVar(0, 9, 'e')
def n = makeIntVar(0, 9, 'n')
def d = makeIntVar(0, 9, 'd')
def m = makeIntVar(1, 9, 'm')
def o = makeIntVar(0, 9, 'o')
def r = makeIntVar(0, 9, 'r')
def y = makeIntVar(0, 9, 'y')
IntVar[] all = [s, e, n, d, m, o, r, y]
IntVar[] scalar = [s, e, n, d, m, o, r, e, m, o, n, e, y]
int[] coeffs = [
1000, 100, 10, 1, // S E N D +
1000, 100, 10, 1, // M O R E =
-10000, -1000, -100, -10, -1 // M O N E Y
]
addConstraint(makeScalProdEquality(scalar, coeffs, 0))
addConstraint(makeAllDifferent(all))
def db = makePhase(all, INT_VAR_DEFAULT, INT_VALUE_DEFAULT)
newSearch(db)
while (nextSolution()) {
println all.join(' ')
}
endSearch()
// Statistics
println "Solutions: ${solutions()}"
println "Failures: ${failures()}"
println "Branches: ${branches()}"
println "Wall time: ${wallTime()}ms"
}运行时它有以下输出
s(9) e(5) n(6) d(7) m(1) o(0) r(8) y(2) Solutions: 1 Failures: 5 Branches: 10 Wall time: 60ms
OR-Tools 是用 C++ 编写的,但有许多语言的接口,包括 Java——这非常适合 Groovy 使用。
Choco 与 JSR331
拥有多个库可供选择是一件好事,但拥有一个标准的 API 可以帮助在这些库之间切换。这就是 JSR331 的用武之地。它定义了一个用于与约束求解器和线性求解器交互的标准 API。在这里,我们使用一个由早期版本的 Choco 库支持的 JSR331 实现。代码如下
import javax.constraints.*
ProblemFactory.newProblem('SEND+MORE=MONEY').with {
def (S, M) = ['S', 'M'].collect { variable(it, 1, 9) }
def (E, N, D, O, R, Y) = ['E', 'N', 'D', 'O', 'R', 'Y'].collect { variable(it, 0, 9) }
postAllDifferent(S, E, N, D, M, O, R, Y)
Var[] ALL = [
S, E, N, D,
M, O, R, E,
M, O, N, E, Y]
int[] COEFFS = [
1000, 100, 10, 1,
1000, 100, 10, 1,
-10000, -1000, -100, -10, -1]
post(COEFFS, ALL, '=', 0)
def solver = getSolver()
def solution = solver.findSolution()
println solution ?: 'No solution'
solver.logStats()
}它与之前的例子非常相似,但现在专门使用 javax.constraint 包中的 JSR331 类。这些类有多个实现支持。因此,确实可以在它们之间切换。运行时,输出是
Solution #1: S[9] M[1] E[5] N[6] D[7] O[0] R[8] Y[2]
话虽如此,在撰写本文时,JSR331 的受欢迎程度似乎并未上升。大多数使用约束编程库的人似乎都在使用直接库类。事实上,JSR331 实现使用的 Choco 实现版本已经有 10 多年了。
纳入进位
我们在前面的例子中使用的标量积全局约束非常强大,可能是我们解决这个问题的首选。但是,我们可以通过多种方式建模约束编程问题,所以让我们来看一个避免使用该全局约束的解决方案。
相反,我们将开发一个模型,该模型反映了我们手动解决原始 TO + GO = OUT 问题时的推理方式。为此,我们只一次考虑一列并考虑进位。我们将在模型中显式引入变量来保存进位(如果没有进位则为 0,如果有进位则为 1)。然后我们将表达适用于每一列的数学约束。
这是代码:
new Model("SEND+MORE=MONEY").with {
def (S, M) = ['S', 'M'].collect { intVar(it, 1, 9) }
def (E, N, D, O, R, Y) = ['E', 'N', 'D', 'O', 'R', 'Y'].collect { intVar(it, 0, 9) }
def C = (0..3).collect{ intVar("C$it", 0, 9) }
allDifferent(S, E, N, D, M, O, R, Y).post()
C[3] .eq(M).post() // C3 C2 C1 C0
C[2].add(S).add(M).eq(O.add(C[3].mul(10))).post() // S E N D
C[1].add(E).add(O).eq(N.add(C[2].mul(10))).post() // M O R E
C[0].add(N).add(R).eq(E.add(C[1].mul(10))).post() // -------------
D .add(E).eq(Y.add(C[0].mul(10))).post() // M O N E Y
println solver.findSolution()
}我们可以看到,现在不再有标量积全局约束,而是每个列的约束。
运行时,输出如下所示
Solution: S=9, M=1, E=5, N=6, D=7, O=0, R=8, Y=2, C0=1, C1=1, C2=0, C3=1, sum_exp_1=9, sum_exp_2=10, (C3*10)=10, sum_exp_3=10, sum_exp_4=6, sum_exp_5=6, (C2*10)=0, sum_exp_6=6, sum_exp_7=7, sum_exp_8=15, (C1*10)=10, sum_exp_9=15, sum_exp_10=12, (C0*10)=10, sum_exp_11=12,
我们可以看到,当我们为每一列定义约束时,模型中会创建子表达式,这些子表达式反映在解决方案中。如果你愿意,它们是获得答案过程中临时的计算——或者更准确地说,是不断变化的临时计算的快照。它们不构成我们感兴趣的答案的一部分,因此如果我们愿意,我们可以自由地只打印出我们感兴趣的解决方案部分。
创建 DSL
前面的例子有很多对 add 和 mul 方法的调用。我们可以创建一点 DSL 来为我们之前的例子提供一些语法糖,以允许使用 Groovy 的运算符重载、支持指定变量域时的范围,以及其他一些优点。我们的代码变为
model("SEND+MORE=MONEY") {
def (S, M) = ['S', 'M'].collect { intVar(it, 1..9) }
def (E, N, D, O, R, Y) = ['E', 'N', 'D', 'O', 'R', 'Y'].collect { intVar(it, 0..9) }
def C = intVarArray(4, 0..1)
[allDifferent(S, E, N, D, M, O, R, Y), // C3 C2 C1 C0
C[3] .eq(M), // S E N D
(C[2] + S + M).eq(O + C[3] * 10), // M O R E
(C[1] + E + O).eq(N + C[2] * 10), // -------------
(C[0] + N + R).eq(E + C[1] * 10), // M O N E Y
(D + E).eq(Y + C[0] * 10)]*.post()
println solver.findSolution()
}它与之前有相同的输出。
您可能想知道求解器是如何找到解决方案的。您可以在调试器中观察变量并使用像 choco-cpviz 这样的工具,但在习惯之前,这是一个相当复杂的过程。我们将尝试让您了解这里发生了什么。基本上,在可能的情况下会有各种剪枝步骤和带有回溯的分支。下面是上面示例的一些快照。
首先,我们有近 90 个浅绿色方块,它们代表了我们的问题搜索空间。我们按照规则寻找剪枝搜索空间的方法

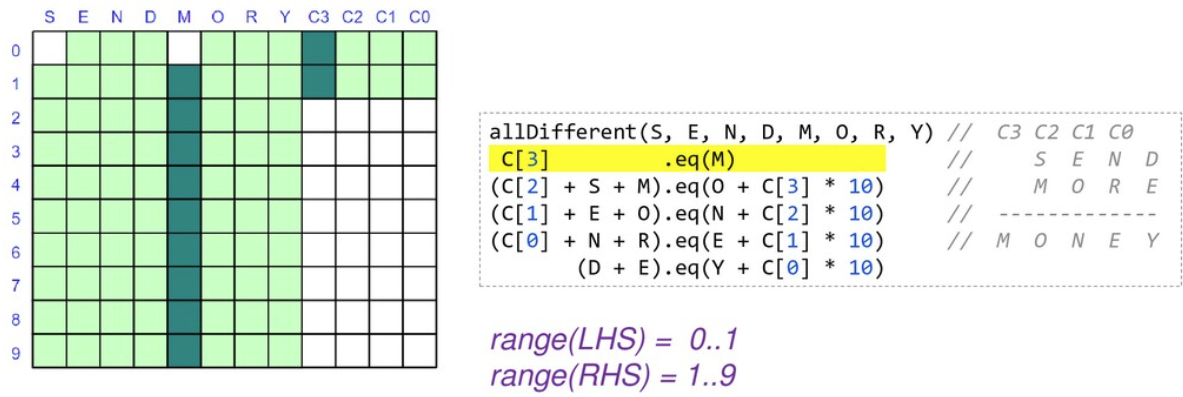


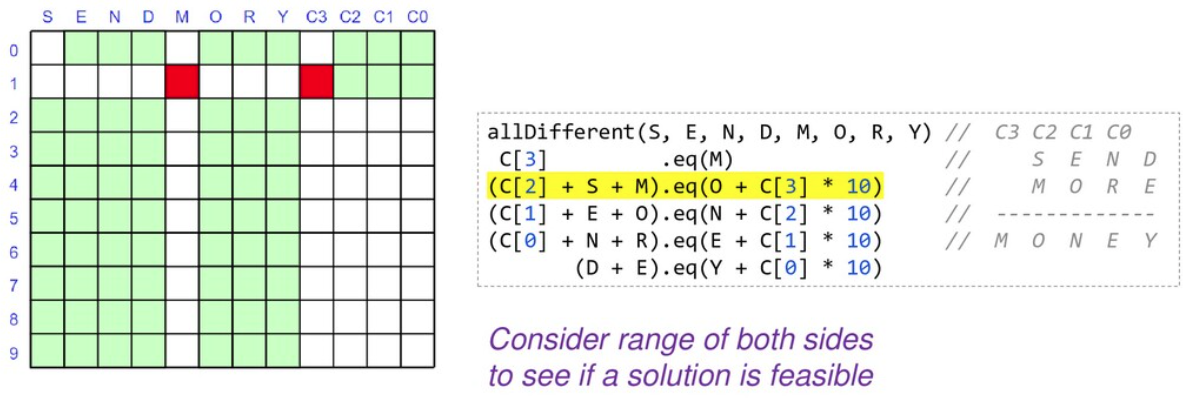
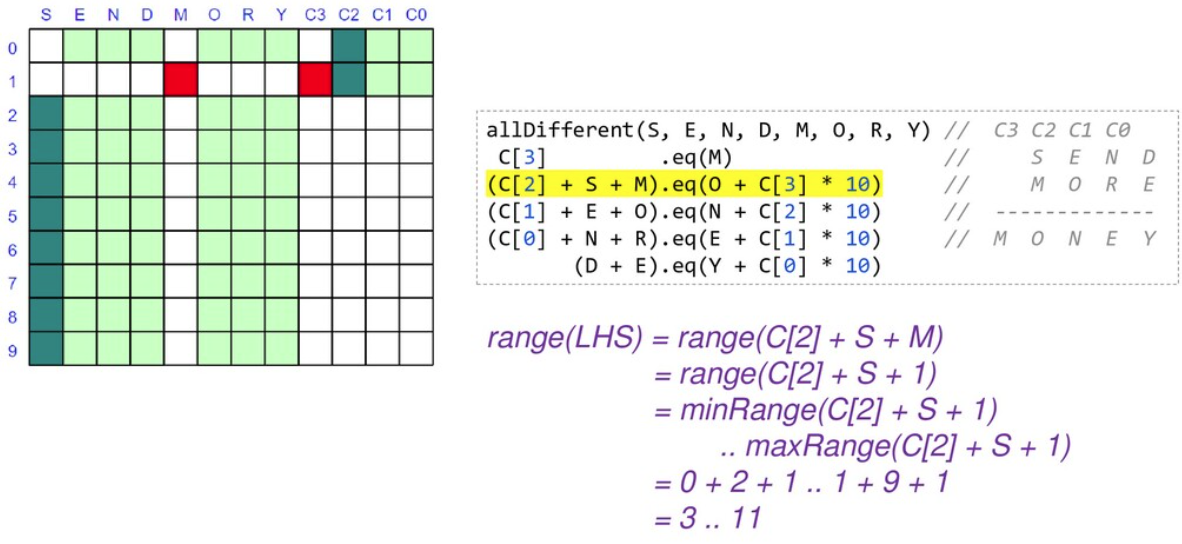



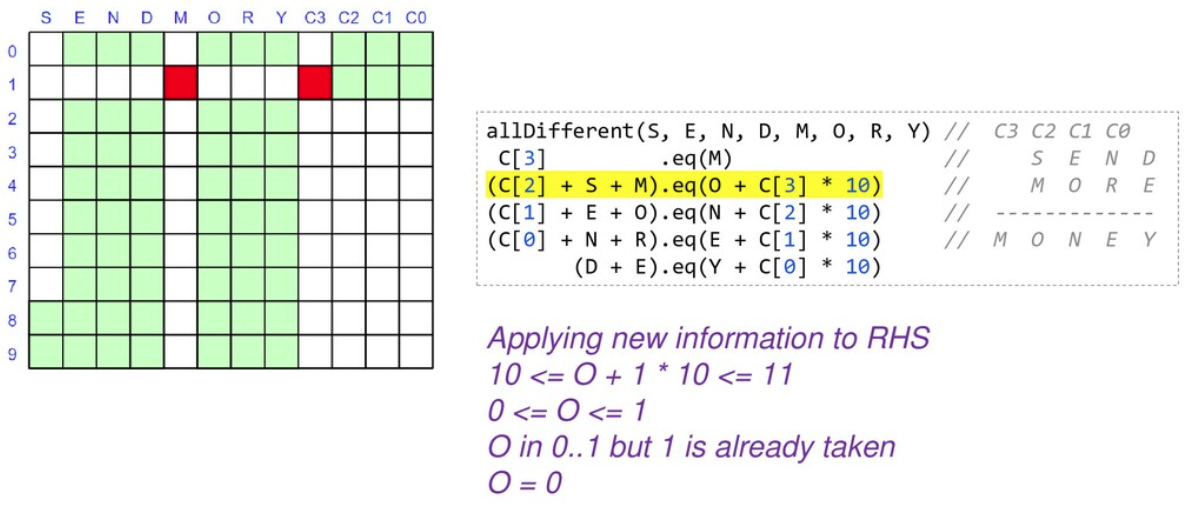
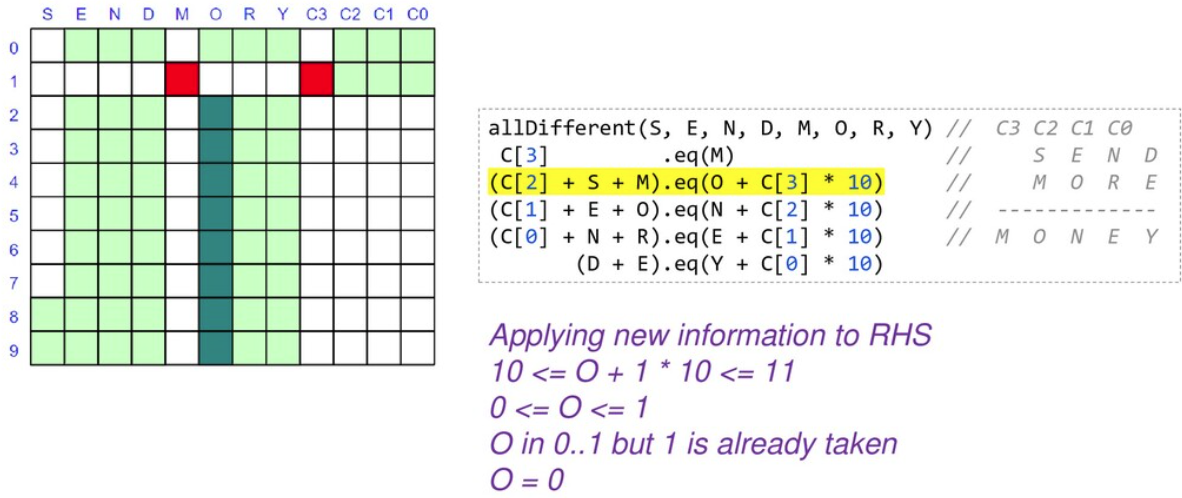
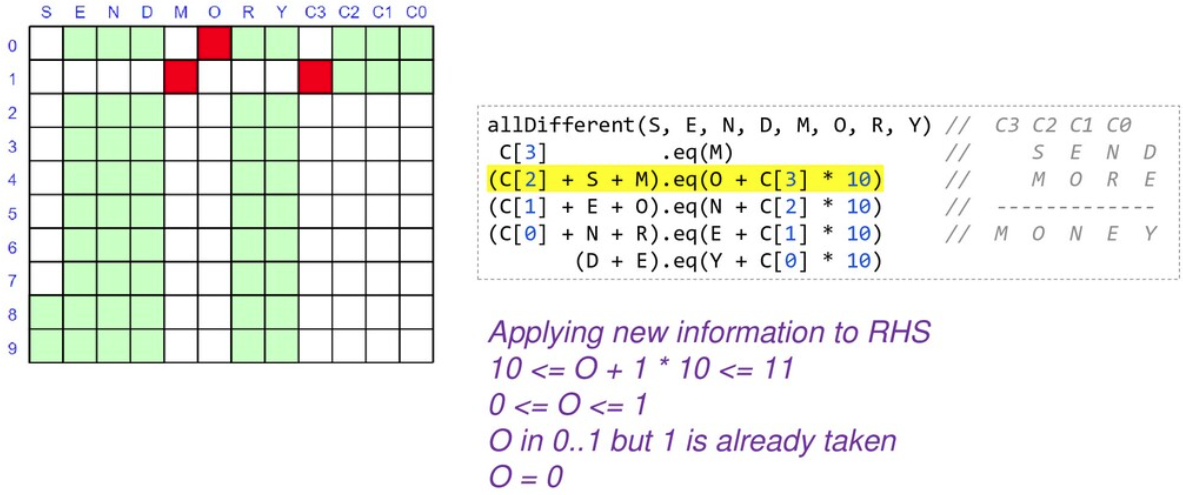

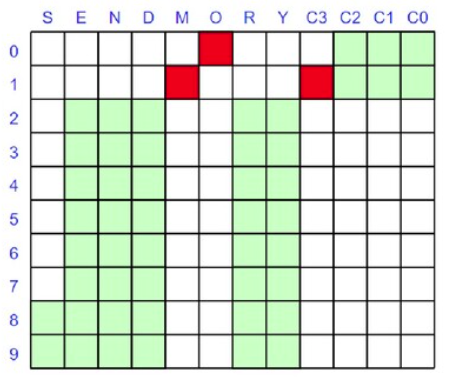
当我们锁定变量的值时,我们可以将其代入并简化我们的约束。当我们重新应用它们时,它们将更快地评估并可能揭示更多信息。
此时我们只有 2 个变量被锁定,但我们的搜索空间几乎是我们开始时的一半,并且我们已经简化了一些约束。此时我们将继续分支和求解,直到找到解决方案或确定没有解决方案。
其他语言
示例仓库还包含其他语言的此问题的解决方案,因此您可以进行比较和对比,包括 Clojure、Haskell (Frege)、Java、JavaScript (Nashorn)、Ruby (JRuby)、Python (Jython)、Kotlin、Lua (Luaj)、Prolog (tuprolog) 和 Scala。

最后,让我们再看几个例子(使用 Choco)。我们将解决一些来自关于密码算术问题历史的有趣博客的例子
-
ABCD * 4 = DCBA -
AA + BB + CC = ABC -
HALF + HALF = WHOLE -
HALF + FIFTH + TENTH + TENTH + TENTH = WHOLE
这是代码:
new Model("ABCD*4=DCBA").with {
def (A, D) = ['A', 'D'].collect { intVar(it, 1, 9) }
def (B, C) = ['B', 'C'].collect { intVar(it, 0, 9) }
def R = (0..2).collect { intVar(0, 9) }
allDifferent(A, B, C, D).post()
R[2].add(A.mul(4)).eq(D).post()
R[1].add(B.mul(4)).eq(C.add(R[2].mul(10))).post()
R[0].add(C.mul(4)).eq(B.add(R[1].mul(10))).post()
D.mul(4).eq(A.add(R[0].mul(10))).post()
solver.findAllSolutions().each {
println "$name: ${pretty(it, [A, B, C, D, ' * 4 = ', D, C, B, A])}\n$it\n"
}
}
new Model("AA+BB+CC=ABC").with {
def (A, B, C) = ['A', 'B', 'C'].collect { intVar(it, 1, 9) }
allDifferent(A, B, C).post()
A.mul(11).add(B.mul(11).add(C.mul(11))).eq(A.mul(100).add(B.mul(10)).add(C)).post()
solver.findAllSolutions().each {
println "$name: ${pretty(it, [A, A, ' + ', B, B, ' + ', C, C, ' = ', A, B, C])}\n$it\n"
}
}
new Model("HALF+HALF=WHOLE").with {
def (H, W) = ['H', 'W'].collect { intVar(it, 1, 9) }
def (A, E, F, L, O) = ['A', 'E', 'F', 'L', 'O'].collect { intVar(it, 0, 9) }
allDifferent(H, W, A, E, F, L, O).post()
IntVar[] ALL = [
H, A, L, F,
W, H, O, L, E]
int[] COEFFS = [
2000, 200, 20, 2,
-10000, -1000, -100, -10, -1]
scalar(ALL, COEFFS, "=", 0).post()
solver.findAllSolutions().each {
println "$name: ${pretty(it, [H, A, L, F, ' + ', H, A, L, F, ' = ', W, H, O, L, E])}\n$it\n"
}
}
new Model("HALF+FIFTH+TENTH+TENTH+TENTH=WHOLE").with {
def (H, F, T, W) = ['H', 'F', 'T', 'W'].collect { intVar(it, 1, 9) }
def (A, L, I, E, N, O) = ['A', 'L', 'I', 'E', 'N', 'O'].collect { intVar(it, 0, 9) }
allDifferent(H, F, T, W, A, L, I, E, N, O).post()
IntVar[] ALL = [
H, A, L, F,
F, I, F, T, H,
T, E, N, T, H,
T, E, N, T, H,
T, E, N, T, H,
W, H, O, L, E]
int[] COEFFS = [
1000, 100, 10, 1,
10000, 1000, 100, 10, 1,
10000, 1000, 100, 10, 1,
10000, 1000, 100, 10, 1,
10000, 1000, 100, 10, 1,
-10000, -1000, -100, -10, -1]
scalar(ALL, COEFFS, "=", 0).post()
solver.findAllSolutions().each {
def parts = [H, A, L, F, '+', F, I, F, T, H, '+', T, E, N, T, H, '+',
T, E, N, T, H, '+', T, E, N, T, H, '=', W, H, O, L, E]
println "$name: ${pretty(it, parts)}\n$it\n"
}
}
// helper method to print solutions
def pretty(model, parts) {
parts.collect { p -> p instanceof IntVar ? model.getIntVal(p) : p }.join()
}其输出如下
ABCD*4=DCBA: 2178 * 4 = 8712 Solution: A=2, D=8, B=1, C=7, IV_1=3, IV_2=3, IV_3=0, (A*4)=8, sum_exp_4=8, (B*4)=4, …, AA+BB+CC=ABC: 11 + 99 + 88 = 198 Solution: A=1, B=9, C=8, (A*11)=11, (B*11)=99, (C*11)=88, …, HALF+HALF=WHOLE: 9604 + 9604 = 19208 Solution: H=9, W=1, A=6, E=8, F=4, L=0, O=2, HALF+HALF=WHOLE: 9703 + 9703 = 19406 Solution: H=9, W=1, A=7, E=6, F=3, L=0, O=4, HALF+HALF=WHOLE: 9802 + 9802 = 19604 Solution: H=9, W=1, A=8, E=4, F=2, L=0, O=6, HALF+FIFTH+TENTH+TENTH+TENTH=WHOLE: 6701+14126+25326+25326+25326=96805 Solution: H=6, F=1, T=2, W=9, A=7, L=0, I=4, E=5, N=3, O=8,
您应该看到解决这些谜题的常见模式。
更多信息
结论
我们已经研究了如何使用 Groovy 和一些约束编程库来解决密码算术谜题。何不尝试解决一些您自己的谜题呢?
