使用 Groovy™、Commons Math、Hipparchus、OptaPlanner 和 Timefold 解决简单的优化问题
发布时间:2024-03-14 晚上 10:22(最后更新时间:2024-12-10 晚上 06:45)
简介
有许多问题涉及优化。我们将探讨一个可以使用线性优化(也称为线性规划)解决的案例研究。线性规划问题在满足一个或多个线性等式和不等式约束的条件下,优化一个特定的线性目标函数。
我们将研究这样一个问题以及可用于解决这些问题的一些库和工具。
案例研究:饮食优化
让我们来看一个案例研究,我们尝试在保持健康或饮食偏好所设定的总体约束的同时,最小化我们饮食中食物的成本。这个例子受到这个 SAS 例子的启发,但有关更详细的线性规划例子(经典的斯蒂格勒饮食问题,使用 Google OR-Tools 解决),请参阅更多信息部分。
首先,以下是构成我们饮食的六种食物及其成本和营养价值
面包 🍞 |
牛奶 🥛 |
奶酪 🧀 |
土豆 🥔 |
鱼 🐟 |
酸奶 🍶 |
|
成本 |
2.0 |
3.5 |
8.0 |
1.5 |
11.0 |
1.0 |
蛋白质 (g) |
4.0 |
8.0 |
7.0 |
1.3 |
8.0 |
9.2 |
脂肪 (g) |
1.0 |
5.0 |
9.0 |
0.1 |
7.0 |
1.0 |
碳水化合物 (g) |
15.0 |
11.7 |
0.4 |
22.6 |
0.0 |
17.0 |
卡路里 |
90 |
120 |
106 |
97 |
130 |
180 |
我们希望在保持最佳营养的同时最小化成本,其中“最佳”将定义为满足以下标准
-
必须至少含有 300 卡路里
-
脂肪不超过 10 克
-
碳水化合物不少于 10 克
-
脂肪不少于 8 克
-
鱼至少 0.5 单位
-
牛奶不超过 1 单位
请注意,我们不推荐将这组简化的约束作为真实的饮食,它仅用于我们案例研究的说明目的。
将此与我们之前对线性规划的定义联系起来,我们上面的列表代表了我们的线性约束。我们的目标函数是成本,由每种食物的数量乘以其成本决定。
使用电子表格求解器解决
这类问题如此常见,甚至在电子表格应用程序中也存在求解器。我们将展示一个使用 Google 表格的 OpenSolver 插件的解决方案。但如果您喜欢,也可以使用 Microsoft Excel 做同样的事情。
首先,我们填写问题的数据。它将类似于下面显示的图,但最初,变量单元格(蓝色)和目标单元格(黄色)将为空白。
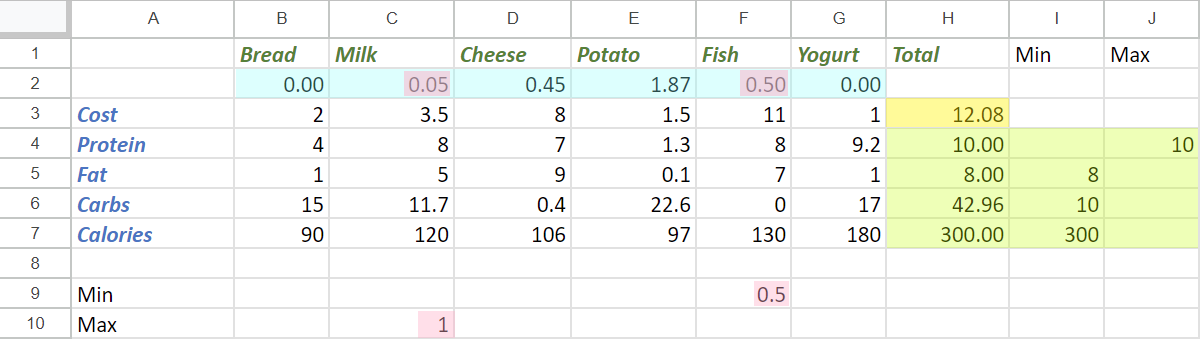
然后,使用 OpenSolver 扩展,我们通过单元格范围识别我们的数据(蓝色)和目标(黄色)单元格,以及约束。
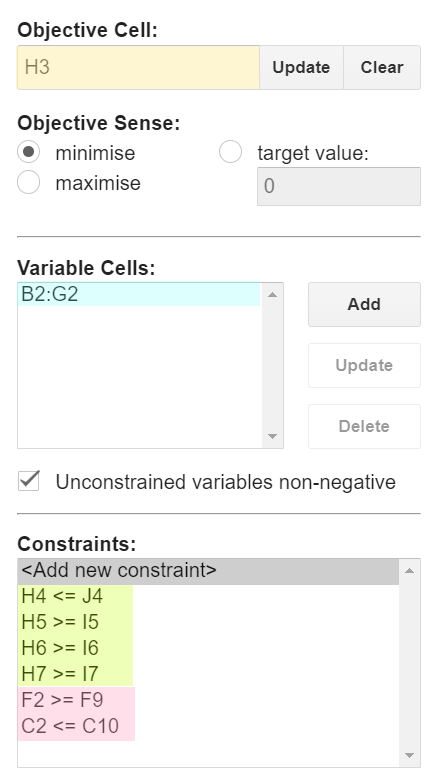
然后我们点击“求解”,它会计算出我们的优化值。
让我们看看如何使用 Groovy 以编程方式解决这个问题。Groovy 为解决此类问题提供了特别好的脚本环境,但对于我们正在使用的库,应该可以使用大多数 JVM 语言。
使用 Apache Commons Math 或 Hipparchus
现在让我们看看如何使用单纯形法求解器解决这个问题。我们将使用 Apache Commons Math 中的 SimplexSolver 类,它与 Hipparchus(Commons Math 的一个分支)中的类基本相同。
我们将从一个用于定义约束的小型辅助方法开始
static scalar(coeffs, rel, double val) {
new LinearConstraint(coeffs as double[], rel, val)
}接下来我们定义我们的单个约束和组合集
var milk_max = scalar([0, 1, 0, 0, 0, 0], LEQ, 1)
var fish_min = scalar([0, 0, 0, 0, 1, 0], GEQ, 0.5)
var protein = scalar([4.0, 8.0, 7.0, 1.3, 8.0, 9.2], LEQ, 10)
var fat = scalar([1.0, 5.0, 9.0, 0.1, 7.0, 1.0], GEQ, 8)
var carbs = scalar([15.0, 11.7, 0.4, 22.6, 0.0, 17.0], GEQ, 10)
var calories = scalar([90, 120, 106, 97, 130, 180], GEQ, 300)
LinearConstraintSet constraints = [milk_max, fish_min, protein, fat, carbs, calories]每个单独的约束都包含每种食物的系数、关系和值。
接下来,我们定义成本函数,以及一个额外的约束,表明我们不能购买负量的任何食物。`zeroOrMore` 约束使我们无需像 `fish_min` 那样冗长地为每种食物设置最小值为 `0`。
var cost = new LinearObjectiveFunction([2.0, 3.5, 8.0, 1.5, 11.0, 1.0] as double[], 0)
var zeroOrMore = new NonNegativeConstraint(true)现在,我们的解决方案是通过创建一个新的求解器,并要求它使用我们的成本函数和约束进行优化来找到的。然后我们将解决方案打印出来
var solution = new SimplexSolver().optimize(cost, constraints, zeroOrMore)
static pretty(int idx, double d) {
d ? [sprintf('%s %.2f', ['🍞', '🥛', '🧀', '🥔', '🐟', '🍶'][idx], d)] : []
}
if (solution != null) {
printf "Cost: %.2f%n", solution.value
println solution.point.indexed().collectMany(this::pretty).join(', ')
}运行时,它给出以下输出
Cost: 12.08 🥛 0.05, 🧀 0.45, 🥔 1.87, 🐟 0.50
这与我们在使用电子表格时看到的解决方案相同。
您目前可以通过切换类路径上使用的 jar 的 Maven 坐标和更改一些导入语句来在 Apache Commons Math 和 Hipparchus 之间进行切换。这在未来的版本中可能会有所改变,但目前
-
使用
org.apache.commons:commons-math3:3.6.1提供了 Commons Math 的一个较旧的稳定版本,已有 8 年历史,开始显现出其年代。 -
使用
org.apache.commons:commons-math4-legacy:4.0-beta1提供了 Apache Commons Math 中这些类的最新版本。命名可能需要一些解释。目前正在努力将 Commons Math 模块化,并因此交付了许多组件。优化类尚未开发,可在上述工件中找到。 -
使用
org.hipparchus:hipparchus-optim:3.1提供了来自分支项目的类。对于我们正在使用的类,该分支基本没有区别,但如果您不介意依赖一个不受 ASF 支持的项目,那么该库的其他部分已经看到了有用的更新。
如果您不喜欢这些选项,还有更多,以下是一些与上述示例位于同一仓库中的 Groovy 解决方案
-
有关在 Google OR-Tools 中使用 SCIP 单纯形求解器的解决方案,请参阅 DietOrTools.groovy
-
有关 SAS 中 Groovy 支持的解决方案,请参阅 DietGroovy.sas
-
有关在 ojAlgo 中使用 LP 求解器的解决方案,请参阅 DietOjalgo.groovy
-
有关使用 Choco 约束编程求解器的解决方案,请参阅 DietChocoInt.groovy(使用缩放整数的解决方案)和 DietChocoReal.groovy(使用 Ibex 集成实现实数的解决方案)
-
有关使用 JaCoP 约束编程求解器的解决方案,请参阅 DietJacopInt.groovy(使用缩放整数的解决方案)和 DietJacopIntKnapsack.groovy(利用背包约束的解决方案)
对于像我们的案例研究这样可以使用单纯形法求解器解决的简单优化问题,您通常无需再深入研究。这是一种解决此类问题的非常有效的方法。对于另一类稍微复杂的问题,它们可以通过一些巧妙的方法映射到线性规划问题。
对于更复杂的问题,通常没有超高效的解决方案方法。您需要运用一系列技术来管理此类问题中固有的潜在巨大搜索空间。这就是 OptaPlanner(和 Timefold)等优化库发挥作用的地方。
使用 OptaPlanner 或 Timefold
OptaPlanner 是一个将优化算法与约束求解相结合的优化库。在过去的十年大部分时间里,该库都是在 Red Hat 的指导下开发的。在过去的 12 个月里,该项目和其他相关项目作为 Apache KIE 的一部分被捐赠给 ASF。最近,该库也被分叉为 Timefold。
在这篇博客中,我们将使用 Timefold,但如您在引用的存储库中所示,示例中的代码在这两个库中保持不变。只是库的 Maven 坐标和相关的类导入发生了变化。目前,尚不清楚这两个项目将如何随时间演变。
Timefold 项目的一个主张是它具有更轻量级的依赖关系。这可以通过在相关构建中运行 `printRuntimeClasspath` 任务来确认。Timefold 有 20 个依赖 jar,而 OptaPlanner 有 55 个 jar。
虽然对于我们的简单问题不需要 Timefold 的强大功能,但让我们看看如何将它用于相同的案例研究。
首先,我们将创建一个规划实体。这是一个求解器知道会随时间变化并包含一个或多个规划变量的类。
在我们的例子中,我们只有一个规划变量,即 `amount` 属性,求解器将在尝试找到最优解时对其进行调整。
@PlanningEntity
@TupleConstructor(includeFields = true)
class Food {
final String name, emoji
final double cost, protein, fat, carbs, calories
@PlanningVariable(valueRangeProviderRefs = "amount")
Integer amount // times 100
}我们使用整数作为 `amount` 的类型,因为整数对于求解器来说更容易处理。我们实际上将存储数量(如前面示例所示)乘以 100,但在显示结果时将除以 100。
一旦在实例构造期间定义,我们类的其他字段就是常量。
接下来,我们定义一个规划解决方案类。这包含有关任何给定解决方案所需的所有信息,包括一个 `score`。分数让我们能够确定一个解决方案是否比另一个更优化,以及给定解决方案是否满足所有硬约束和软约束(稍后解释)。
@PlanningSolution
class DietSolution {
@PlanningEntityCollectionProperty
List<Food> foods
@ValueRangeProvider(id = "amount")
CountableValueRange<Integer> getAmount() {
ValueRangeFactory.createIntValueRange(0, 200, 5)
}
@PlanningScore
HardSoftScore score
String toString() {
var sb = new StringBuilder()
foods.eachWithIndex { f, idx ->
sb << "$f.emoji $f.name: ${f.amount / 100}\n"
}
for (name in ['fat', 'carbs', 'protein', 'calories', 'cost']) {
var total = foods.sum{ f -> f."$name" * f.amount / 100 }
sb << sprintf("Total %s: %.2f%n", name, total)
}
sb << "Score: $score"
sb
}
}接下来我们想定义一些约束。通常,我们有必须满足的硬约束和如果可能就应该满足的软约束。在我们的例子中,我们将有诸如各种食物和各种营养指标的最小值和最大值等约束。
class DietConstraintProvider implements ConstraintProvider {
@Override
Constraint[] defineConstraints(ConstraintFactory factory) {
new Constraint[]{
maxField(factory, 'protein', 10),
minField(factory, 'fat', 8),
minField(factory, 'carbs', 10),
minField(factory, 'calories', 300),
minFood(factory, 'Fish', 50),
maxFood(factory, 'Milk', 100),
minCost(factory),
}
}
private static int amountOf(Food f, String name) {
(f."$name" * f.amount).toInteger()
}
private static Constraint minField(ConstraintFactory factory, String fieldName, double minAmount) {
ToIntFunction<Food> amount = f -> amountOf(f, fieldName)
factory.forEach(Food)
.groupBy(sum(amount))
.filter(fs -> fs < minAmount * 100)
.penalize(ONE_HARD)
.asConstraint("Min $fieldName")
}
private static Constraint maxField(ConstraintFactory factory, String fieldName, double maxAmount) {
ToIntFunction<Food> amount = f -> amountOf(f, fieldName)
factory.forEach(Food)
.groupBy(sum(amount))
.filter(fs -> fs > maxAmount * 100)
.penalize(ONE_HARD)
.asConstraint("Max $fieldName")
}
private static Constraint minFood(ConstraintFactory factory, String foodName, double minAmount) {
factory.forEach(Food)
.filter(f -> f.name == foodName && f.amount < minAmount)
.penalize(ONE_HARD)
.asConstraint("Min $foodName")
}
private static Constraint maxFood(ConstraintFactory factory, String foodName, double maxAmount) {
factory.forEach(Food)
.filter(f -> f.name == foodName && f.amount > maxAmount)
.penalize(ONE_HARD)
.asConstraint("Max $foodName")
}
private static ToIntFunction<Food> totalCost = f ->
(f.cost * f.amount).toInteger()
private static Constraint minCost(ConstraintFactory factory) {
factory.forEach(Food)
.filter(f -> f.amount > 0)
.groupBy(sum(totalCost))
.penalize(ONE_SOFT, fs -> fs >> 2)
.asConstraint('Min cost')
}
}有了这些辅助类,我们现在可以
def unsolved = new DietSolution(foods: [
new Food('Bread' , '🍞', 2.0, 4.0, 1.0, 15.0, 90),
new Food('Milk' , '🥛', 3.5, 8.0, 5.0, 11.7, 120),
new Food('Cheese', '🧀', 8.0, 7.0, 9.0, 0.4, 106),
new Food('Potato', '🥔', 1.5, 1.3, 0.1, 22.6, 97),
new Food('Fish' , '🐟', 11.0, 8.0, 7.0, 0.0, 130),
new Food('Yogurt', '🍶', 1.0, 9.2, 1.0, 17.0, 180)
])
def config = new SolverConfig()
.withSolutionClass(DietSolution)
.withEntityClasses(Food)
.withConstraintProviderClass(DietConstraintProvider)
.withTerminationSpentLimit(Duration.ofSeconds(10))
def factory = SolverFactory.create(config)
def solver = factory.buildSolver()
println solver.solve(unsolved)运行时它有以下输出
08:17:05.202 [main] INFO a.t.s.core.impl.solver.DefaultSolver - Solving started: time spent (25), best score (-6init/0hard/0soft), environment mode (REPRODUCIBLE), move thread count (NONE), random (JDK with seed 0). 08:17:05.385 [main] INFO a.t.s.c.i.c.DefaultConstructionHeuristicPhase - Construction Heuristic phase (0) ended: time spent (210), best score (-1hard/-521soft), score calculation speed (1355/sec), step total (6). 08:17:15.175 [main] INFO a.t.s.c.i.l.DefaultLocalSearchPhase - Local Search phase (1) ended: time spent (10000), best score (-1hard/-261soft), score calculation speed (155967/sec), step total (1030). 08:17:15.176 [main] INFO a.t.s.core.impl.solver.DefaultSolver - Solving ended: time spent (10000), best score (-1hard/-261soft), score calculation speed (152685/sec), phase total (2), environment mode (REPRODUCIBLE), move thread count (NONE). 🍞 Bread: 0.6 🥛 Milk: 0.6 🧀 Cheese: 0 🥔 Potato: 0.4 🐟 Fish: 0.5 🍶 Yogurt: 1.05 Total fat: 8.19 Total carbs: 42.91 Total protein: 21.38 Total calories: 418.80 Total cost: 10.45 Score: -1hard/-261soft
考虑到我们给求解器的时间,并使用默认的搜索算法,我们甚至无法满足所有硬约束。搜索空间如此广阔,以至于我们从未到达搜索空间中所有约束都得到满足的区域。
好消息是我们可以提供额外的指导,以便求解器在搜索过程中朝着更好的方向前进。以下是一种可能的额外配置,以及更新后的 `config` 定义
def construction = new ConstructionHeuristicPhaseConfig(
constructionHeuristicType: FIRST_FIT)
def moveSelector = new UnionMoveSelectorConfig([
new ChangeMoveSelectorConfig(),
new SwapMoveSelectorConfig()
])
def localSearch = new LocalSearchPhaseConfig(
localSearchType: VARIABLE_NEIGHBORHOOD_DESCENT,
moveSelectorConfig: moveSelector)
def config = new SolverConfig()
.withSolutionClass(DietSolution)
.withEntityClasses(Food)
.withConstraintProviderClass(DietConstraintProvider)
.withPhases(construction, localSearch) // additional solution guidance
.withTerminationSpentLimit(Duration.ofSeconds(10))它现在运行时有以下输出
🍞 Bread: 0 🥛 Milk: 0 🧀 Cheese: 0.5 🥔 Potato: 1.9 🐟 Fish: 0.5 🍶 Yogurt: 0 Total fat: 8.19 Total carbs: 43.14 Total protein: 9.97 Total calories: 302.30 Total cost: 12.35 Score: 0hard/-308soft
我们可以在这里看到,它现在接近线性规划的结果。
更多信息
-
OR-Tools 线性优化
-
一个基于 斯蒂格勒饮食 问题的相关但更详细的例子,使用 Google OR-Tools
-
一个 Python 饮食例子,也使用 Google OR-Tools
-
包含示例代码的 GitHub 仓库
Diet DietOptaPlanner DietTimefold
结论
我们研究了如何使用 Groovy 和一些线性优化库来解决饮食案例研究。我们的主要关注点是 Apache Commons Math 和 Hipparchus 库。我们还探索了使用更强大的 Timefold 和 OptaPlanner 库。
