使用 Groovy™、Apache Commons Math、ojAlgo、Nd4j 和 EJML 进行矩阵计算
发布时间:2022-08-18 01:41PM
本博客探讨使用 Groovy 和各种库进行矩阵计算:Apache Commons Math、ojAlgo、EJML 和 Nd4j(Eclipse Deeplearning4j 的一部分)。我们还将快速了解如何使用孵化中的 Vector API 进行矩阵计算(JEP 338、414、417 和 426)。
斐波那契数列
斐波那契数列起源于几个世纪前的印度,但以 1202 年出版的《计算之书》的意大利作者命名。在该出版物中,斐波那契提出该数列作为计算理想化(生物学上不现实)兔子种群增长的一种方法。他提出,将一对新生的可繁殖兔子放入田地中;每对可繁殖兔子在一个月大时交配,并在第二个月末总是产下另一对兔子;兔子从不死去,而是永远繁殖。斐波那契提出了一个难题:一年内会有多少对兔子?数列是这样的
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233
我们可以使用矩阵来解决这个问题。如果我们将矩阵 ![]() 自身相乘 n 次,我们将得到
自身相乘 n 次,我们将得到 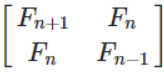 。这是一种称为矩阵幂的运算。让我们使用四个最流行且维护良好的矩阵库来探索这个问题。
。这是一种称为矩阵幂的运算。让我们使用四个最流行且维护良好的矩阵库来探索这个问题。
Apache Commons Math
让我们探索使用 Apache Commons Math 解决这个问题。Apache Commons Math 是一个轻量级的独立数学和统计组件库。矩阵是该库线性代数部分的一部分,在这种情况下,双精度值矩阵是相关的。因此,我们将斐波那契数列表示为双精度值。
double[][] data = [[1d, 1d], [1d, 0d]]
def m = MatrixUtils.createRealMatrix(data)
println m * m * m
println m**6Commons Math 有一个工厂方法,用于从双精度数组创建矩阵。乘法和幂运算方法的名称恰好与 Groovy 可用于运算符重载的方法(即 multiply 和 power)对齐,因此我们可以使用 Groovy 方便的速记。
当我们运行脚本时,输出如下所示
Array2DRowRealMatrix{{3.0,2.0},{2.0,1.0}}
Array2DRowRealMatrix{{13.0,8.0},{8.0,5.0}}
我们可以更进一步,打印矩阵中的值,但结果已经足够清楚了。我们看到斐波那契数列中的值出现在输出中。
EJML
EJML(高效 Java 矩阵库)是一个用于操作实数、复数、密集和稀疏矩阵的线性代数库。它也是一个 100% Java 解决方案。它具有一些新颖的特性,包括从 Matlab 导入和支持半环(GraphBLAS),可用于图算法,其中稀疏矩阵可用作图的邻接矩阵或关联矩阵。
我们可以使用 EJML 进行相同的计算
def m = new SimpleMatrix([[1d, 1d], [1d, 0d]] as double[][])
def ans = m.mult(m).mult(m)
println ans
6.times { ans = ans.mult(m) }
println ans乘法方法的名称与我们可以使用自动运算符重载速记的方法不同,所以我们只需调用 EJML 提供的方法。稍后在语言可扩展性部分,我们将看到如何实际添加支持以使用与 Commons Math 相同的速记。
EJML 没有幂运算方法,但我们只需调用乘法所需次数即可达到相同的效果。请注意,我们增加了第二个矩阵的迭代次数,以显示斐波那契数列的下一组元素。
运行此脚本的输出如下
Type = DDRM , rows = 2 , cols = 2 3.0000E+00 2.0000E+00 2.0000E+00 1.0000E+00 Type = DDRM , rows = 2 , cols = 2 5.5000E+01 3.4000E+01 3.4000E+01 2.1000E+01
第一个矩阵的数字与之前相同,第二个矩阵显示了斐波那契数列中的下一个数字(21、34 和 55)。
Nd4j
Nd4j 为 Java 用户提供了 Python 中的功能。它包含了 numpy 操作和 tensorflow/pytorch 操作的组合。Nd4j 利用本地后端,使其能够在不同平台上工作,并在扩展时提供高效的操作。
我们斐波那契解决方案的代码与 EJML 非常相似
def m = Nd4j.create([[1, 1], [1, 0]] as int[][])
def ans = m.mmul(m).mmul(m)
println ans
9.times { ans = ans.mmul(m) }
println ans与前两个库不同的是,Nd4j 支持整数矩阵(以及双精度数和许多其他数值及相关类型)。
运行脚本得到以下输出
...
[main] INFO org.nd4j.linalg.factory.Nd4jBackend - Loaded [CpuBackend] backend
...
[main] INFO org.nd4j.linalg.cpu.nativecpu.CpuNDArrayFactory - Binary level Generic x86 optimization level AVX/AVX2
[main] INFO org.nd4j.linalg.api.ops.executioner.DefaultOpExecutioner - Blas vendor: [OPENBLAS]
...
[[ 3, 2],
[ 2, 1]]
[[ 233, 144],
[ 144, 89]]
同样,第一个矩阵与我们之前看到的相同,第二个矩阵在斐波那契数列中又增加了三个元素。
ojAlgo
我们将要看的下一个库是 ojAlgo(oj! Algorithms)。它是一个开源的全 Java 产品,用于数学、线性代数和优化,支持数据科学、机器学习和科学计算。它声称是可用的最快的纯 Java 线性代数库,项目网站提供了许多支持该说法的基准测试链接。
这是我们斐波那契示例的代码
def factory = Primitive64Matrix.FACTORY
def m = factory.rows([[1d, 1d], [1d, 0d]] as double[][])
println m * m * m
println m**15我们可以看到它支持我们为 Commons Math 看到的相同的运算符重载特性。
当我们运行脚本时,它有以下输出
org.ojalgo.matrix.Primitive64Matrix < 2 x 2 >
{ { 3.0, 2.0 },
{ 2.0, 1.0 } }
org.ojalgo.matrix.Primitive64Matrix < 2 x 2 >
{ { 987.0, 610.0 },
{ 610.0, 377.0 } }
正如预期的那样,第一个矩阵与我们之前看到的相同,而第二个矩阵显示了序列中的后三个数字。
探索 Vector API 和 EJML
从 JDK16 开始,各种版本的 Vector API(JEP 338、414、417、426)已作为孵化中的预览功能提供。HotSpot 编译器此前已经有一些最小的优化可以利用矢量硬件指令,但 Vector API 极大地扩展了可能优化的范围。我们可以尝试编写自己的代码,利用 Vector API 并可能自己执行矩阵乘法。但是,其中一个库已经这样做了,所以我们将探索这条路径。
EJML 库的主要贡献者发布了一个 仓库,用于非常早期的原型设计和基准测试。我们将使用其一个类中的方法来探索 Vector API 在我们的斐波那契示例中的使用。MatrixMultiplication 类有三个方法:mult_ikj_simple 的编码方式就像我们任何人第一次从其定义编写乘法方法时,没有尝试任何优化;mult_ikj 以高度优化的方式编码,并对应于 EJML 通常使用的代码;mult_ikj_vector 使用 Vector API。请注意,您可以将这些方法视为比我们在前一个示例中调用的 mult 方法“低一层”,即我们之前使用的 mult 方法将在底层调用其中一个。这就是为什么我们传递内部“矩阵”表示而不是我们的 SimpleMatrix 实例。
对于我们的小计算,Vector API 提供的优化预计不会很大。但是,我们将为所有库生成矩阵的计算作为第一步,并且我们将对这三种方法(mult_ikj_simple、mult_ikj 和 mult_ikj_vector)进行 1000 次迭代的循环计算。代码如下所示
def m = new SimpleMatrix([[1, 1], [1, 0]] as double[][])
double[] expected = [3, 2, 2, 1]
def step1, result
long t0 = System.nanoTime()
1000.times {
step1 = new SimpleMatrix(2, 2)
result = new SimpleMatrix(2, 2)
MatrixMultiplication.mult_ikj_simple(m.matrix, m.matrix, step1.matrix)
MatrixMultiplication.mult_ikj_simple(step1.matrix, m.matrix, result.matrix)
assert result.matrix.data == expected
}
long t1 = System.nanoTime()
1000.times {
step1 = new SimpleMatrix(2, 2)
result = new SimpleMatrix(2, 2)
MatrixMultiplication.mult_ikj(m.matrix, m.matrix, step1.matrix)
MatrixMultiplication.mult_ikj(step1.matrix, m.matrix, result.matrix)
assert result.matrix.data == expected
}
long t2 = System.nanoTime()
1000.times {
step1 = new SimpleMatrix(2, 2)
result = new SimpleMatrix(2, 2)
MatrixMultiplication.mult_ikj_vector(m.matrix, m.matrix, step1.matrix)
MatrixMultiplication.mult_ikj_vector(step1.matrix, m.matrix, result.matrix)
assert result.matrix.data == expected
}
long t3 = System.nanoTime()
printf "Simple: %6.2f ms\n", (t1 - t0)/1000_000
printf "Optimized: %6.2f ms\n", (t2 - t1)/1000_000
printf "Vector: %6.2f ms\n", (t3 - t2)/1000_000此示例在 JDK16 上运行,使用以下 VM 选项:–enable-preview –add-modules jdk.incubator.vector。
输出如下
WARNING: Using incubator modules: jdk.incubator.vector
Simple: 116.34 ms
Optimized: 34.91 ms
Vector: 21.94 ms
我们在这里可以看到,即使对于我们微不足道的计算,也取得了一些改进。当然,对于更大的问题,使用 Vector API 的好处可能会相当可观。
莱斯利矩阵
早些时候,我们将斐波那契数列描述为用于不现实的兔子种群,其中兔子永不死亡并永远繁殖。事实证明,斐波那契矩阵是更通用模型的一种特殊情况,该模型可以模拟现实的兔子种群(以及其他事物)。这些是 莱斯利矩阵。对于莱斯利矩阵,种群被分为多个类别,我们跟踪每个类别在特定时期内的出生率和存活率。我们将这些信息以特殊形式存储在矩阵中。下个时期的每个类别的种群可以通过乘以莱斯利矩阵从当前时期的种群中计算出来。
这种技术可用于动物种群或人类种群计算。莱斯利矩阵可以帮助您确定是否有足够的 X 世代、千禧一代和 Z 世代纳税人来支持老龄化且即将退休的婴儿潮一代人口。复杂的动物模型可能会跟踪某种动物及其捕食者或猎物的种群。存活率和出生率可能会根据这些信息进行调整。鉴于只有雌性会生育,莱斯利模型通常只考虑雌性种群,然后从中推断出总种群。
我们将根据此关于莱斯利矩阵的视频教程展示一个袋鼠种群的示例。它可以帮助我们了解袋鼠种群是否受到威胁(也许干旱、火灾或洪水影响了它们的觅食栖息地),或者有利条件是否导致了过度繁殖。
根据该示例,我们将袋鼠分为 3 个种群类别:0 至 3 岁、3 至 6 岁和 6 至 9 岁。我们每三年观察一次种群。0-3 岁年龄组的出生率 (B1) 为 0,因为它们是未达到生育年龄的。最肥沃的 3-6 岁年龄组的出生率 (B2) 为 2.3。老年袋鼠(6-9 岁)的出生率 (B3) 为 0.4。我们假设没有袋鼠能活过 9 岁。60% (S1) 的幼年袋鼠能存活到下一个年龄组。30% (S2) 的中年袋鼠能存活到老年。最初,每个年龄组有 400 只袋鼠。
这是此模型的代码
double[] init = [400, // 0..<3
400, // 3..<6
400] // 6..9
def p0 = MatrixUtils.createRealVector(init)
println "Initial populations: $p0"
double[][] data = [
[0 , 2.3, 0.4], // B1 B2 B3
[0.6, 0, 0 ], // S1 0 0
[0 , 0.3, 0 ] // 0 S2 0
]
def L = MatrixUtils.createRealMatrix(data)
def p1 = L.operate(p0)
println "Population after 1 round: $p1"
def p2 = L.operate(p1)
println "Population after 2 rounds: $p2"
def L10 = L ** 10
println "Population after 10 rounds: ${L10.operate(p0).toArray()*.round()}"此代码产生以下输出
Initial populations: {400; 400; 400}
Population after 1 round: {1,080; 240; 120}
Population after 2 rounds: {600; 648; 72}
Population after 10 rounds: [3019, 2558, 365]
第一轮过后,我们看到了许多幼袋鼠,但老年组的数量令人担忧地下降。第二轮过后,只有最年长的年龄组看起来小得令人担忧。然而,由于年轻一代数量健康,我们可以看到,经过 10 代后,总人口确实没有危险。事实上,人口过剩可能会成为一个问题。
矩阵加密
早期加密消息的一种技术是凯撒密码。它通过将字母表中的字母按一定量移位来替换字母,例如“IBM”如果移位到前一个字母则变为“HAL”,如果字母表向前移位一个字母则“VMS”变为“WNT”。这种密码可以通过查看字母或模式词的频率分析来破解。
希尔密码通过将多个字母分解到加密文本的每个字母中来改进凯撒密码。使用矩阵使得同时处理三个或更多符号变得实用。通常,一个 N×N 矩阵(密钥)与消息的矩阵形式编码相乘。结果是加密文本的矩阵表示(编码形式)。我们使用密钥的逆矩阵来解密消息。
我们需要一种方法来将文本消息转换为矩阵,然后再从矩阵转换回来。一个常见的方案是将 A 编码为 1,B 编码为 2,依此类推。我们只使用每个字符的 ASCII 值。我们定义 encode 和 decode 方法来执行此操作
double[][] encode(String s) { s.bytes*.intValue().collate(3) as double[][] }
String decode(double[] data) { data*.round() as char[] }我们将定义一个 2x2 矩阵作为密钥并用它进行加密。我们将找到密钥的逆矩阵并用它进行解密。如果需要,我们可以使用 3x3 密钥以提高安全性,但代价是处理时间更长。
我们的代码是这样的
def message = 'GROOVY'
def m = new SimpleMatrix(encode(message))
println "Original: $message"
def enKey = new SimpleMatrix([[1, 3], [-1, 2]] as double[][])
def encrypted = enKey.mult(m)
println "Encrypted: ${decode(encrypted.matrix.data)}"
def deKey = enKey.invert()
def decrypted = deKey.mult(encrypted)
println "Decrypted: ${decode(decrypted.matrix.data)}"运行时,它有以下输出
Original: GROOVY Encrypted: ĴŔŚWZc Decrypted: GROOVY
这比凯撒密码提供了更多的安全性,然而,鉴于当今的计算能力,希尔密码仍然可以通过足够的暴力破解最终被破解。因此,希尔密码很少单独用于加密,但它们经常与其他技术结合使用以增加扩散——增强其他技术提供的安全性。
形状操作
我们的最后一个例子着眼于几何变换形状。为此,我们将形状的点表示为向量,并使用表示为矩阵的变换来乘以它们。我们只需要担心角落,因为我们将使用 Swing 来绘制我们的形状,它有一个方法可以通过给出其角落来绘制多边形。
首先,我们将使用 Groovy 的 SwingBuilder 来设置我们的框架
new SwingBuilder().edt {
def frame = frame(title: 'Shapes', size: [420, 440], show: true, defaultCloseOperation: DISPOSE_ON_CLOSE) {
//contentPane.background = Color.WHITE
widget(new CustomPaintComponent())
}
frame.contentPane.background = Color.WHITE
}我们在这里并没有真正使用 SwingBuilder 的太多功能,但如果我们要添加更多功能,SwingBuilder 会让这项任务变得更容易。
我们将在自定义组件中实际绘制我们的形状。我们将定义一些颜色常量,一个 drawPolygon 方法,给定一个点矩阵,它将这些点绘制成一个多边形。我们还将定义一个 vectors 方法将点列表(角点)转换为向量,以及一个 transform 方法,它是一个用于创建变换矩阵的工厂方法。
这是代码:
class CustomPaintComponent extends Component {
static final Color violet = new Color(0x67, 0x27, 0x7A, 127)
static final Color seaGreen = new Color(0x69, 0xCC, 0x67, 127)
static final Color crystalBlue = new Color(0x06, 0x4B, 0x93, 127)
static drawPolygon(Graphics g, List pts, boolean fill) {
def poly = new Polygon().tap {
pts.each {
addPoint(*it.toRawCopy1D()*.round()*.intValue().collect { it + 200 })
}
}
fill ? g.fillPolygon(poly) : g.drawPolygon(poly)
}
static List<Primitive64Matrix> vectors(List<Integer>... pts) {
pts.collect{ factory.column(*it) }
}
static transform(List<Number>... lists) {
factory.rows(lists as double[][])
}
void paint(Graphics g) {
g.drawLine(0, 200, 400, 200)
g.drawLine(200, 0, 200, 400)
g.stroke = new BasicStroke(2)
def triangle = vectors([-85, -150], [-145, -30], [-25, -30])
g.color = seaGreen
drawPolygon(g, triangle, true)
// transform triangle
...
def rectangle = vectors([0, -110], [0, -45], [95, -45], [95, -110])
g.color = crystalBlue
drawPolygon(g, rectangle, true)
// transform rectangle
...
def trapezoid = vectors([50, 50], [70, 100], [100, 100], [120, 50])
g.color = violet
drawPolygon(g, trapezoid, true)
// transform trapezoid
...
}
}当我们运行此代码时,我们看到了三个形状
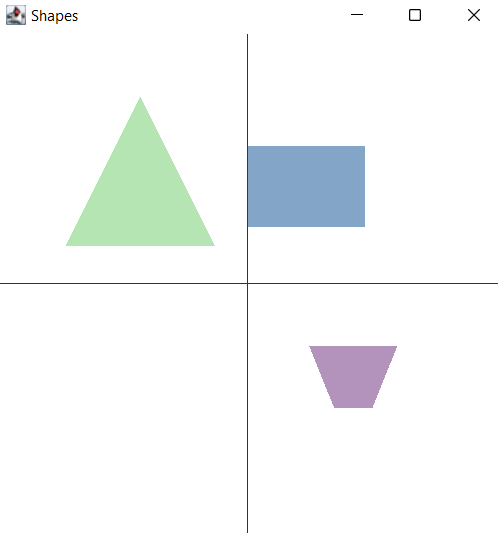
现在我们可以添加变换了。我们将有一个逆时针旋转 90 度的变换。另一个将形状放大 25%,一个将形状缩小 25%。我们可以通过将变换相乘来简单地组合变换。我们将对三角形进行两次变换。两种情况下都旋转,但一个缩小,另一个放大。我们只需将每个点乘以变换矩阵即可应用变换。然后我们将两个变换后的形状绘制成轮廓而不是填充(为了更容易区分原始版本和变换版本)。这是代码
def rot90 = transform([0, 1], [-1, 0])
def bigger = transform([1.25, 0], [0, 1.25])
def smaller = transform([0.75, 0], [0, 0.75])
def triangle_ = triangle.collect{ rot90 * bigger * it }
drawPolygon(g, triangle_, false)
triangle_ = triangle.collect{ rot90 * smaller * it }
drawPolygon(g, triangle_, false)对于我们的矩形,我们将有一个简单的变换,它在垂直轴上翻转形状。第二个变换将多个更改组合在一个变换中。我们可以将其拆分为更小的变换然后将它们相乘——但这里它们都在一个中。我们在水平轴上翻转然后应用剪切。然后我们将变换后的形状绘制成轮廓
def flipV = transform([1, 0], [0, -1])
def rectangle_ = rectangle.collect{ flipV * it }
drawPolygon(g, rectangle_, false)
def flipH_shear = transform([-1, 0.5], [0, 1])
rectangle_ = rectangle.collect{ flipH_shear * it }
drawPolygon(g, rectangle_, false)对于我们的梯形,我们创建一个逆时针旋转 45 度的变换(回想一下 sin 45° = cos 45° = 0.707)。然后我们创建 6 个变换,分别旋转 45、90、135 度等。我们将每个变换后的形状绘制成轮廓
def rot45 = transform([0.707, 0.707], [-0.707, 0.707])
def trapezoid_
(1..6).each { z ->
trapezoid_ = trapezoid.collect{ rot45 ** z * it }
drawPolygon(g, trapezoid_, false)
}当我们运行整个示例时,输出如下所示
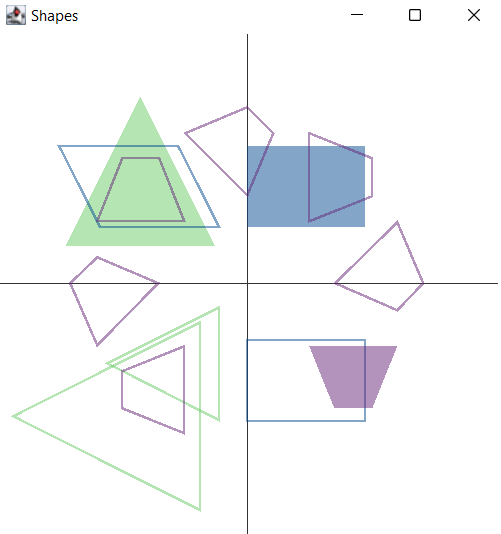
我们在这里可以看到,矩阵变换为我们提供了强大的图像操作方式。我们在这里使用了二维图像,但同样的技术也适用于三维形状。
语言和工具扩展性
我们之前看到,有些示例可以使用 Groovy 运算符速记语法,而另一些则不能。以下是库中一些常见方法的总结
Groovy 运算符 |
+ |
- |
* |
** |
Groovy 方法 |
加 |
减 |
乘 |
幂 |
Commons Math |
|
|
|
|
EJML |
|
|
|
- |
Nd4j |
|
|
|
- |
ojAlgo |
|
|
|
|
如果库使用的名称与 Groovy 的方法相同,则可以使用速记。
Groovy 提供了许多可扩展性功能。我们不会深入探讨所有细节,而是将读者指向Groovy 历史论文,该论文提供了更多细节。
总而言之,该论文为 Commons Math 矩阵定义了以下扩展
RealMatrix.metaClass {
plus << { RealMatrix ma -> delegate.add(ma) }
plus << { double d -> delegate.scalarAdd(d) }
multiply { double d -> delegate.scalarMultiply(d) }
bitwiseNegate { -> new LUDecomposition(delegate).solver.inverse }
constructor = { List l -> MatrixUtils.createRealMatrix(l as double[][]) }
}这修正了上表中一些方法名称不一致的问题。我们现在可以使用运算符速记进行矩阵和标量加法以及标量乘法。我们还可以使用 ~ (bitwiseNegate) 运算符来查找逆。矩阵构造时提到 double[][] 的问题也已解决。
该论文继续讨论如何自动为矩阵库添加必要的导入并根据需要提供别名。本博客的代码清单中未显示导入,但在示例代码仓库的清单中。无论如何,如论文所述,导入可以“配置掉”。最终结果是我们的完整代码可以看起来像这样
var m = [[1, 1], [1, 0]] as Matrix
m**6该论文还讨论了工具的可扩展性,特别是 GroovyConsole 的可视化方面。它展示了如何定义一个输出转换,该转换使用 jlatexmath 库渲染任何矩阵结果。因此,用户不再看到 Array2DRowRealMatrix{{13.0,8.0},{8.0,5.0}},而是看到矩阵的图形渲染。因此,使用 GroovyConsole 时的最终用户体验如下所示
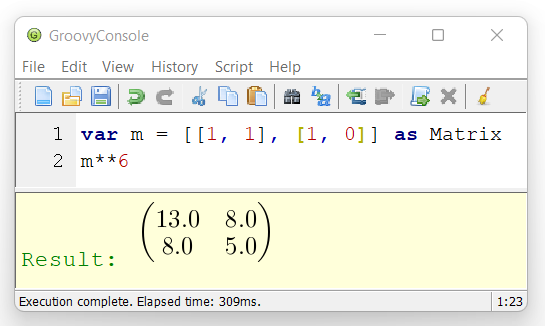
在 Jupyter 风格的环境中,可能支持其他漂亮的输出样式。
更多信息
结论
我们使用 Groovy 编程语言和 Apache Commons Math、ojAlgo、Nd4j 和 EJML 库,探讨了矩阵的一些简单应用。您应该相信,在 JVM 上使用矩阵并不困难,并且您有多种选择。我们还简要了解了 Vector API,这看起来是 JVM 的一个令人兴奋的补充(希望很快以非预览模式推出)。
